Surface Second Harmonic Generation (SHG)

Surface second harmonic generation [1] (SHG) is a coherent, nonlinear optical technique that is well suited for investigations of interfaces. SHG is surface specific due to the intrinsic symmetry constraints on the nonlinear process. Since second harmonic (SH) is produced only in non-centrosymmetric media, there is no SH response from the bulk isotropic materials, but an SH response is obtained at the interface where the symmetry is broken. By using a tunable laser system, we take advantage of the resonant enhancement of the SHG process with an electronic transition. This leads to high sensitivity and specificity in investigating the molecular composition on the surface at the interface. Since the SHG process is intensity dependent, a tunable femtosecond laser system provides the ideal source for surface SHG, allowing for enhanced resonant SH at fluences low enough in order to prevent surface damage. We use a Spectra Physics Solstice Ace equipped with an Optical Parametric Amplifier, capable of delivering 100 fs pulses at 1 kHz in the UV-IR region between 190 - 12,000 nm. This allows to select electronic resonances for the molecular species of interest, with the only limitation imposed by the ability of detecting the second harmonic (down to ~200nm). Using our fast intensified cameras, we can record single shot hyper-spectral images.

Furthermore, we can extend the capability of surface measurement using non-degenerate pumping. This is the case of surface sum frequency mixing (SFM). As shown in Fig. 1 [2], the two pump beams of frequencies w1 and w2 generate the frequency w1+w2 at the interaction with the surface. If one the pump beams is resonant with a transition in the molecular species on the interfacial surface, the SFM signal is enhanced accordingly, allowing for both high specificity and sensitivity in the surface molecular detection. We note that the surface SHG is a particular case of the surface SFM method.

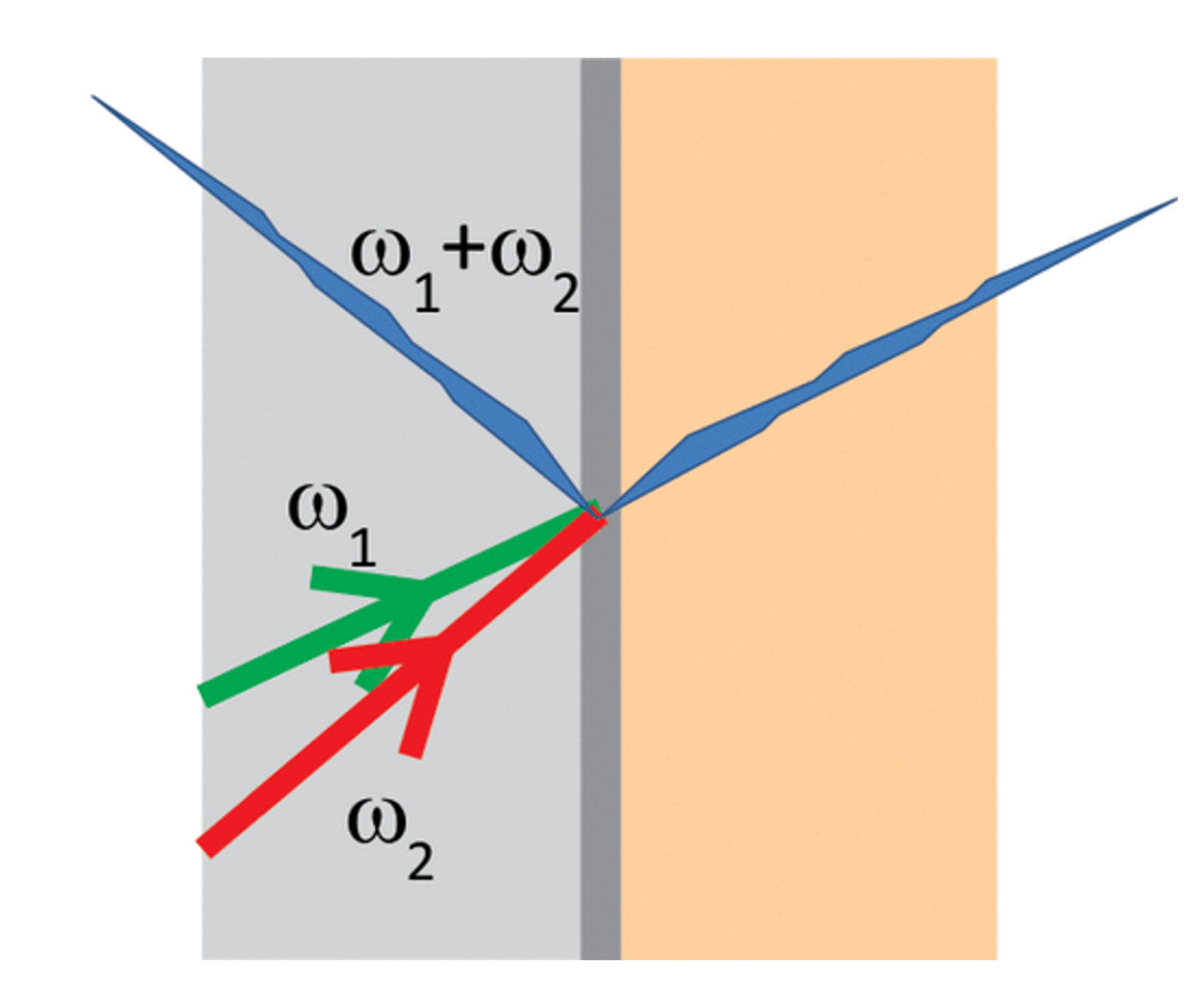
Fig. 1. Surface sum frequency mixing [2].

[1] Terhune, R. W.; Maker, P. D.; Savage, C. M. (1962). "Optical Harmonic Generation in Calcite". Physical Review Letters. 8 (10): 404–406

[2] Y. R. Shen, “Basic Theory of Surface Sum-Frequency Generation,” J.  Phys. Chem. C 2012 116 (29), 15505-15509