Thomson, Raman, and Rayleigh scattering
Advanced Diagnostics Navigation
- Atomic and molecular species, positive and negative ions
- Laser-Induced Fluorescence (LIF) and Two-Photon Absorption LIF (TALIF)
- Radar Resonant Enhanced Multi-Photon Ionization (Radar REMPI)
- Characterization of plasma, chemical composition and dynamic behavior
- Electron velocity distribution function, gas flow velocity and temperature
- Electric field and space potential
- Nanoparticle Diagnostics
- Surface Diagnostics
Thomson, Raman, and Rayleigh scattering
Point measurements of plasma density and temperature (Thomson), molecular vibrational temperature (Raman), and gas temperature (Rayleigh)
Sensitivity threshold for plasma density via Thomson: ne ≥ 109 cm-3
Spatial resolution ~200 μm, temporal resolution 10-20 ns
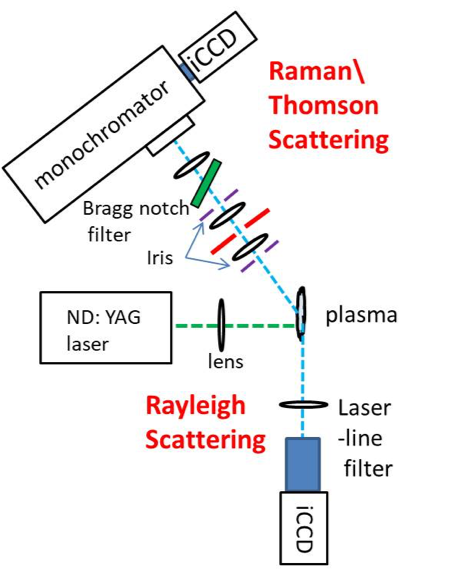
Laser Thomson scattering (LTS) is commonly employed to measure the electron density and electron energy distribution function (EDF). The LTS signal is elastic scattering of laser beam on free electrons which is Doppler broadened due to the velocity of electrons. Recently the plasma density detection limit about 109 cm-3 was reported. We intend to use a volume Bragg notch filter in order to filter the strong Raleigh component from the scattered light. The filter is a reflecting volume Bragg grating (VBG) and is specified to block light with an optical density (OD4) with a full width at half maximum (FWHM) of 5–8 cm−1 (≡0.14–0.23 nm). The transmission of the filter outside the blocking region is 80%. The reflected wavelength can be tuned by rotating the filter. Setting an angle of 6◦ between the filter normal and the direction of the incoming light results in the reflection of 532 nm light, which is the operating wavelength of the laser. In molecular gases the obtained signal contains component of Thomson scattering from electrons and Raman scattering from molecules. The Thomson component is analyzed to obtain electron temperature (broadening) and density (intensity) and Raman component is analyzed for vibrational temperature of molecules. Thomson and Raman scattering with VBG filter is a point technique with spatial resolution of 100-300 µm and temporal resolution ~10-20 ns.
It is possible to measure gas temperature in spatially constricted plasma sources ( such as atmospheric jets for example) using the Rayleigh scattering signal. The intensity of elastically scattered photons (i.e. Rayleigh signal) is in direct proportion to the density of scattering gas. In case of ideal gas this density is inversely proportional to gas temperature, via ideal gas law p=nk_BT_g where p is the given constant pressure, n is the number density of the gas and T_g is the temperature of the gas. The Rayleigh signal is then related to the gas temperature via I_{Rayleigh}\sim n_g = \frac{p}{k_BT_g}. To find the absolute value of T_g we must perform a reference measurement at a known temperature T_{ref}. When gas employed in the reference measurement is identical to the gas in the experiment (or at least has a similar differential cross section for Rayleigh scattering), as are the experimental setup and pressure we can infer that T_g=T_{ref}\frac{I_{ref}}{I_{Rayleigh}}. We assume that major scatter will be the background gas and the addition of species ablated from the target or electrodes will have a negligible contribution due to low densities, when compared to the background gas. Planar geometry of the laser beam can also be used, thus allowing to capture a 2D temperature distribution (in axial and radial directions), with iCCD camera, as a detector.
This capability is located at the Princeton Plasma Physics Laboratory.
